レッドストーン回路には無限の可能性があり、複雑な動作をするものも工夫次第で作れますが、なかなか難解で手を出せないという方も多いのでは?
手始めに、単純な計算機を作りながら練習してみませんか。もちろん現実の回路よりはずっと動きは遅いですし、実用的なものにはなりません。しかし、自分で組んだ大きな回路が動いて正しい計算をしてくれる、というのはロマンがあります。
必要な知識をどこよりも分かりやすく丁寧に書いていくので、ぜひチャレンジしていただきたいと思います!また、何かご質問などがあれば下のコメント欄に書いていただいてかまいませんので、分からない部分は確認しながら読んでくださいね。
目次
この記事を読む前に
もしレッドストーン回路を始めたばかりだという場合は、計算機を作るのはさすがに難しい内容だと思います。以下の記事を読んで、レッドストーン回路の基本について理解しておきましょう。
計算機の成り立ち
まず、計算機とレッドストーン回路にどのような関係があるのかを理解しましょう。
レッドストーン回路は、入力を操作すると、どのような動作をするかを決めるために作るとも言うことができます。
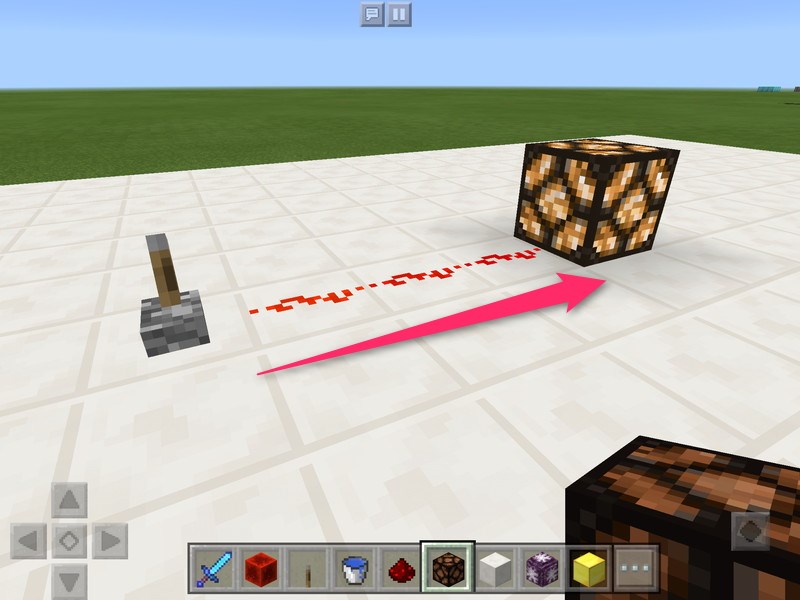
例えば、「レバーをONにするとランプがつく」という回路。このような動作になるのは、レバーとランプをつないだ回路を作ったからですよね。これだけだとかなり簡単な回路ですが、考え方は計算機と全く変わりません。

計算機も、数字などのボタンを押せば正しい計算結果を出してくれるという動作をしますが、実はそれはそういう動作をする回路を上手く作ったから、というだけのことなのです。
そうは言っても、その回路をどうすれば作ることができるのかがまだ分かりませんよね。このためには2つの予備知識がいるので、簡単に説明していきます。
真理値表
真理値表(しんりちひょう)とは、論理回路の入力がどんなときに、どんな出力になるかを示す表のことです。計算機を作るときには、この表を書いて考えると分かりやすくなります。
……なんて説明しても分かりにくいと思いますので、例を見ていきましょう。
NOT回路の真理値表
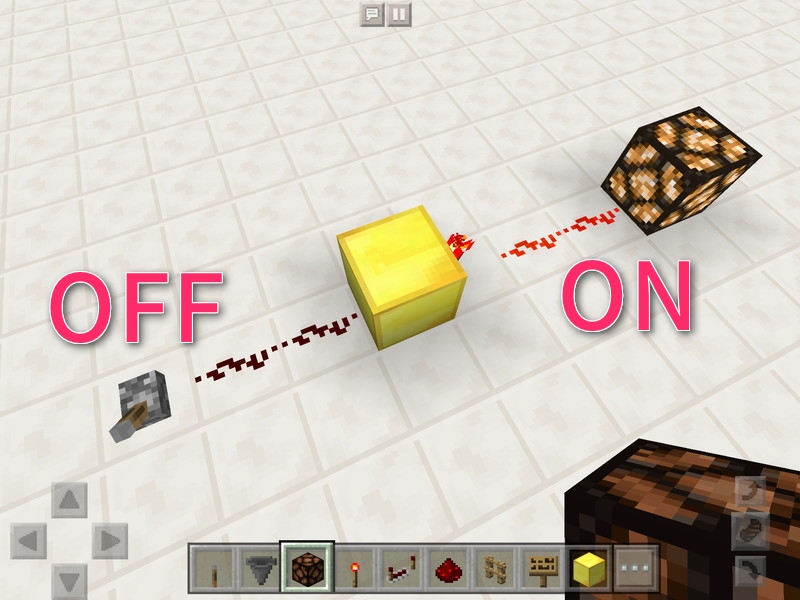
例えばNOT回路は、入力がOFFのとき、出力がONになりますよね。
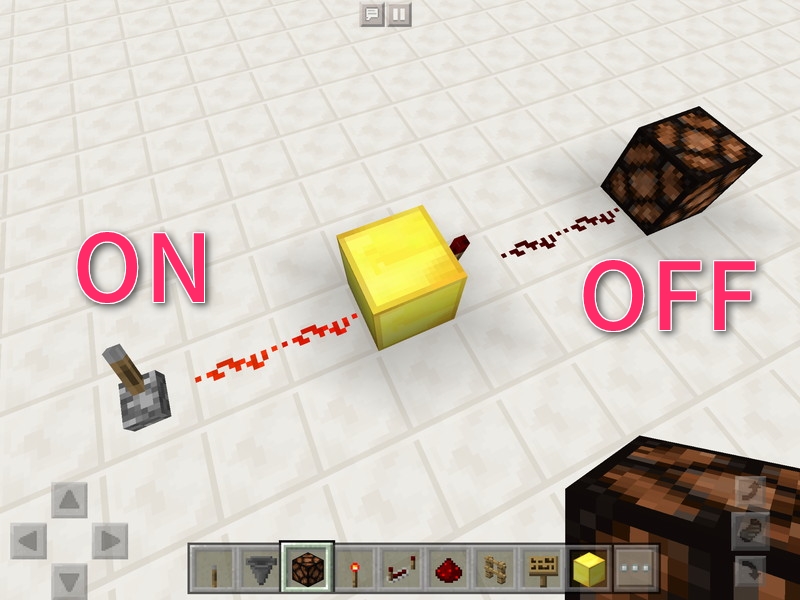
逆に入力がONのとき出力がOFFになります。この入力と出力を表で表現すると……
| 入力 | 出力 |
|---|---|
| OFF | ON |
| ON | OFF |
このようになりますね。しかし、OFFは0、ONは1と書いたほうが便利なので、書き換えましょう(なぜ便利なのかはこの記事を読んでいけばわかります)。
| 入力 | 出力 |
|---|---|
| 0 | 1 |
| 1 | 0 |
0と1が書かれた表ができましたが、これが真理値表と呼ばれるものです。入力が0の時には出力が1に、出力が1の時には入力が0になる、というのが、表を見れば分かりますね。
つまり、NOT回路がどんな動作をするのかを表で表現したというだけです。意外と簡単でしょう。
OR回路の真理値表
OR回路はNOT回路と違って、入力が2つあります。それでも真理値表は書くことができますよ。
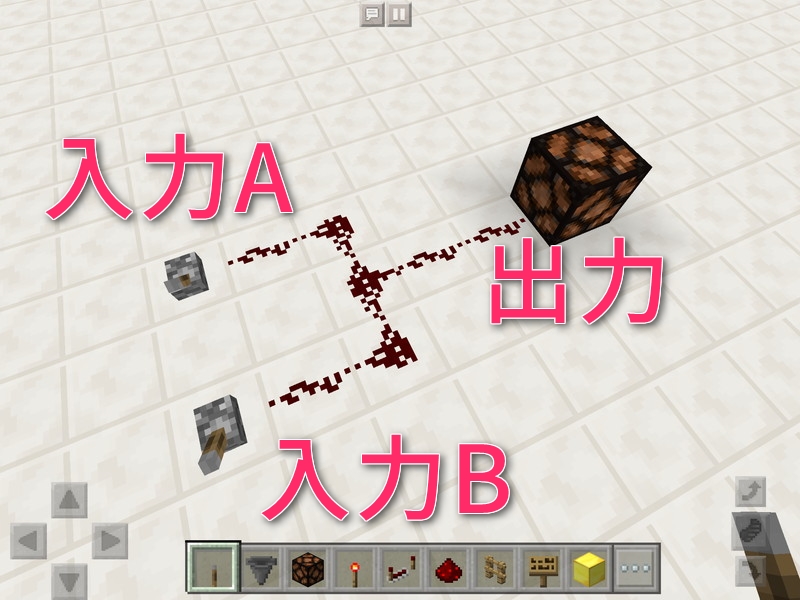
まず入力を区別するために、それぞれ入力A、入力Bと名前をつけます。あとはNOT回路でやったように、それぞれの入力がON、またはOFFの場合の出力を調べていきます。
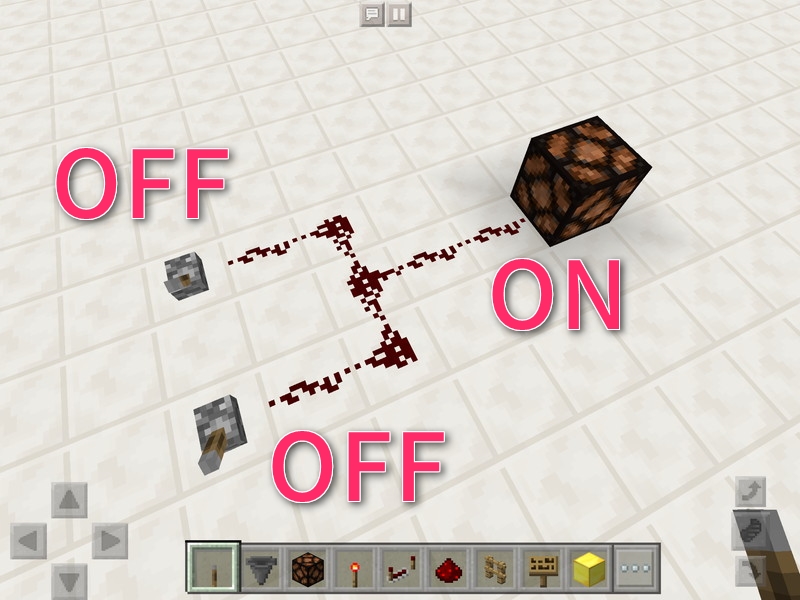
入力AがOFF、入力BがOFFのとき、出力はOFF。

入力AがOFF、入力BがONのとき、出力はON。
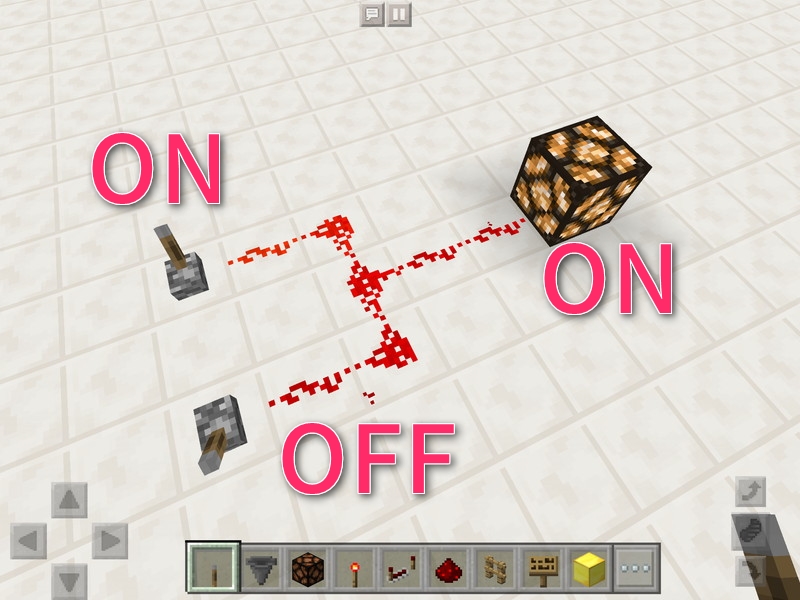
入力AがON、入力BがOFFのとき、出力はON。
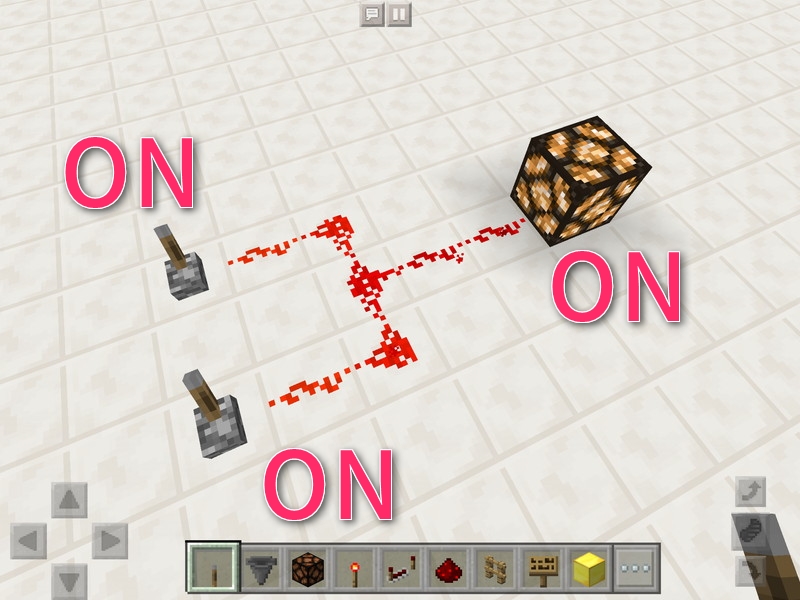
入力AがON、入力BがONのとき、出力はON。これらの結果を真理値表にまとめると、次のようになります。
| 入力A | 入力B | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
入力Aと入力BのONとOFFの組み合わせは4通りあるので、表は4行必要になりましたが、先ほどと同じように真理値表を書くことができました。
それぞれの行を見ると、それぞれの場合に出力がどうなるのか分かるということですね。
AND回路の真理値表
AND回路も、OR回路と同じく入力が2つです。
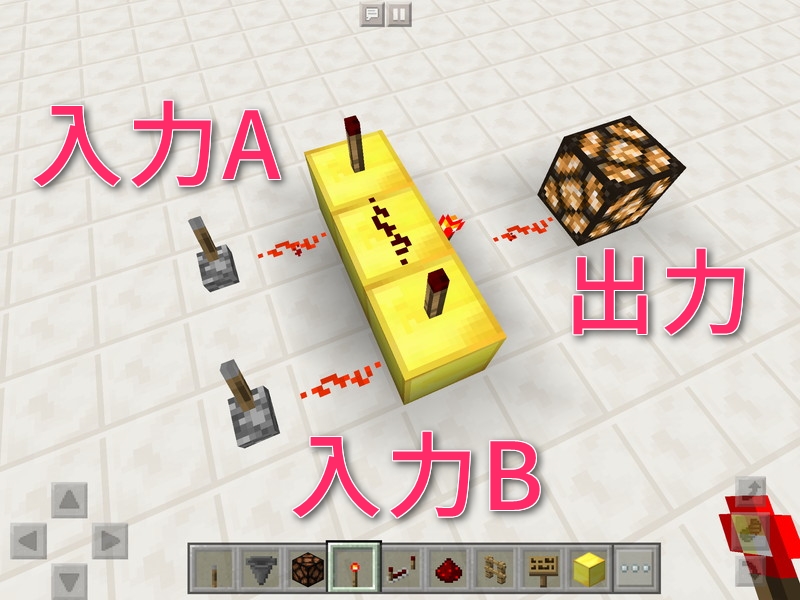
今度は真理値表がどのようになるのか予想してみてください。
正解は以下のようになります。
| 入力A | 入力B | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
出力が1になる行は1つだけ、入力が両方とも1のときですね。AND回路は両方の入力がONのときだけONを出力する回路ですから、この真理値表が正しいことがわかりました。
それは、計算機を作るときには、まず真理値表を先に書いたほうがいいからです。どのような入力のときにどのような出力をするのかを先に決めておけば、どのような回路を作ればいいのかが分かるわけです。これは後で実際にやってみます。
2進数
もう1つだけ知識のお話をさせてください。計算機で数字を取り扱うときにどうするかを考えていきましょう。
2進数が必要な理由
計算機を作るときには、回路で数字を取り扱う必要がある……つまり、回路で数字をどうやって表すのかを決める必要がありますね。
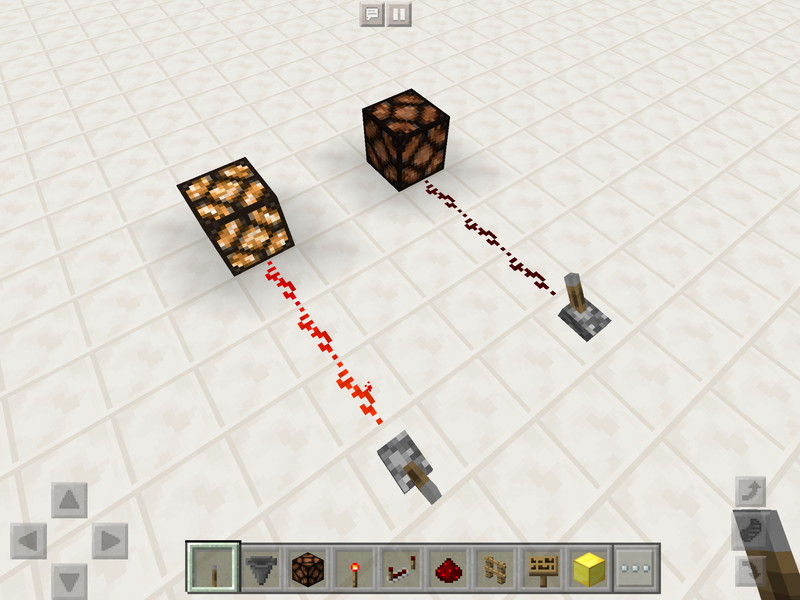
しかし、回路で表せるのはONかOFFだけ。つまり1と0という2種類の数字だけ(※)です。コンピューターは1と0で動いている、などとよく言われますが、その話と同じです。
しかし、私たちがいつも使っている数の数え方(10進数)では0〜9までの10種類の数字を使っています。それに対して、数字が2種類だけでは全然足りませんね。でも、2進数を使えば大丈夫です!
2進数の数え方
2進数は、ONとOFFの2種類の情報しか表せない回路に合わせて、1と0の数字しか使わずに表された数のことです。
私たちがいつも使っている10進法では、「9」の次の数が「10」になります。これは、「9」の次の数字が存在しないので、より大きな数を表すには桁上げ(繰り上がり)をしようという考え方だということは、算数で習ったはず。

2進法でも同じ考え方です。「1」の次の数が「10」になります。「1」の次の数字が存在しない(※)ので、より大きな数を表すには桁上げ(繰り上がり)をしようという考え方なんですね。
| 10進数 | 2進数 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 | … | … |
10進数と2進数で、同じ数を横に並べた表です。
最も単純な計算機を作る
4つの計算ができるようにする
以上、「真理値表」と「2進数」については分かったかと思います。この2つの知識を使うと、単純な計算機をすぐに作ることができます。ここでの単純な計算機とは、以下の4つの計算ができるもののことです。
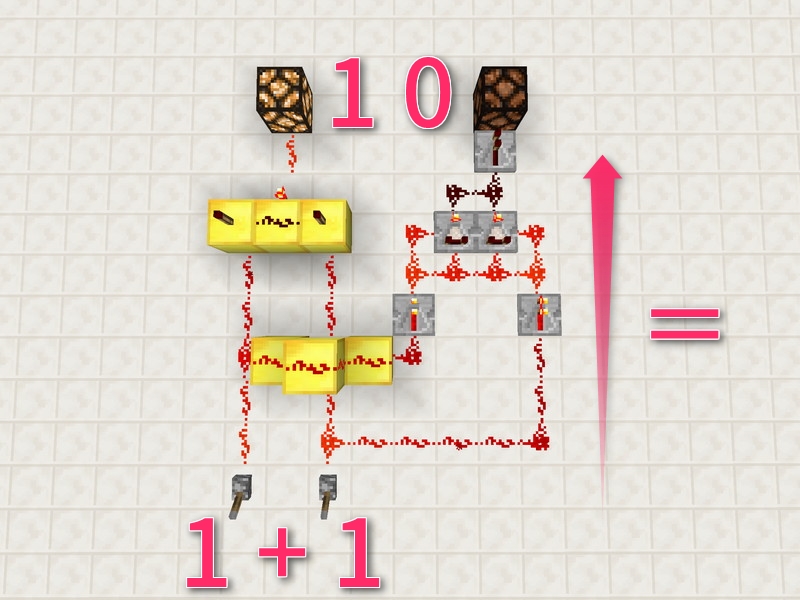
- 0+0=0
- 0+1=1
- 1+0=1
- 1+1=10
ただし、この計算の数字はすべて2進数で表していることに注意してください。特に「1+1=10」というのは、10進法に慣れているとおかしく見えますが、これは先ほど説明したように、2進法では1の次の数字は10だから「1+1=10」だ、ということですよ。
しかし、こんな4つの計算なんて暗算でもできますし、計算機なんか作ってやる必要があるのかと思われるかもしれませんね。しかし、まずはこれを回路で自動的に計算できるように作るということが重要なのです。桁数を増やすといった工夫がしたければ、後でできますから。
必要な入力と出力の数を考える
さて、先ほどの4つの計算、
- 0+0=0
- 0+1=1
- 1+0=1
- 1+1=10
を全てするために必要な入力と出力はいくつになるのか、最初に考えます。回路の形を考えるにしても、入力と出力の数が分からないと話にならないからです。
まず、入力は2つ必要になります。
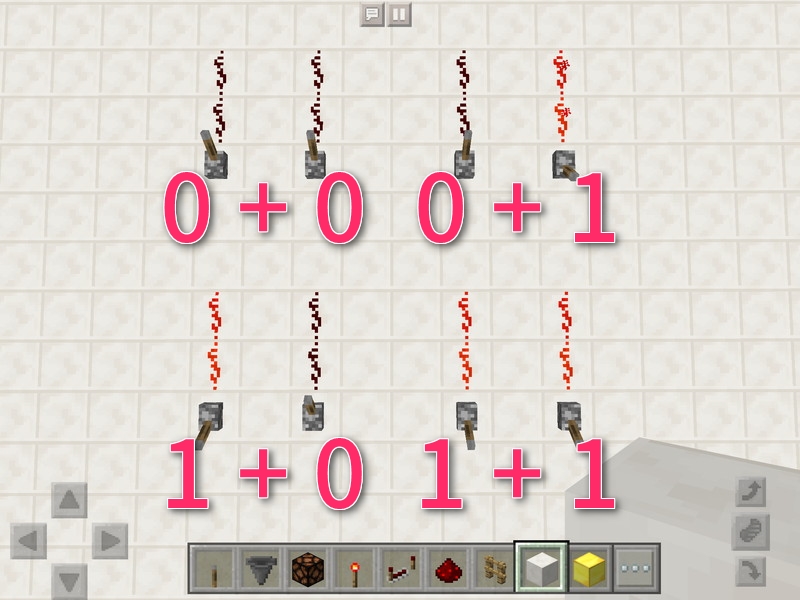
なぜなら、「0+0」「0+1」「1+0」「1+1」という4通りの計算は、画像のように2つのレバーのONとOFFで表せるからです。
そして、出力も2つ必要になります。

なぜなら、「0」「1」「10」という3通りの結果は、画像のように2つのランプのONとOFFで表せるからです。
よって、入力と出力は2つずつ必要になることが分かりました。これを回路にすると、以下の画像のようになります。
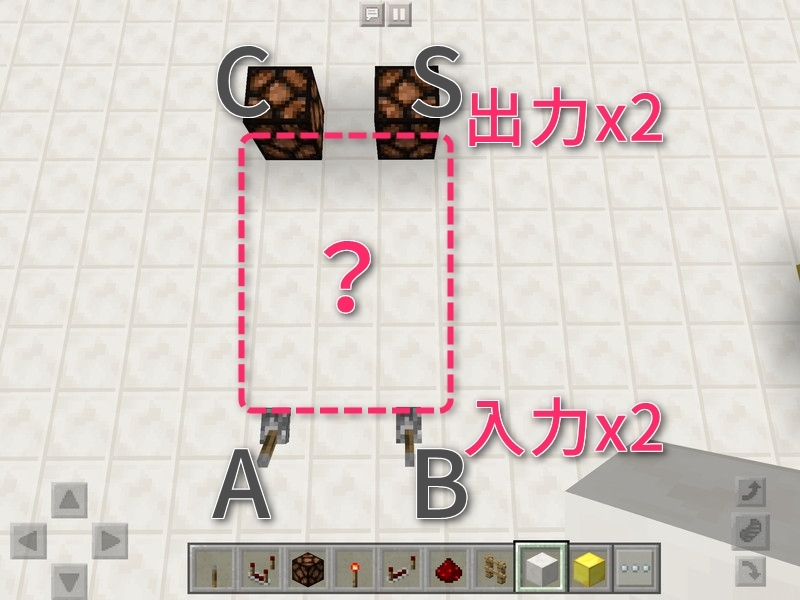
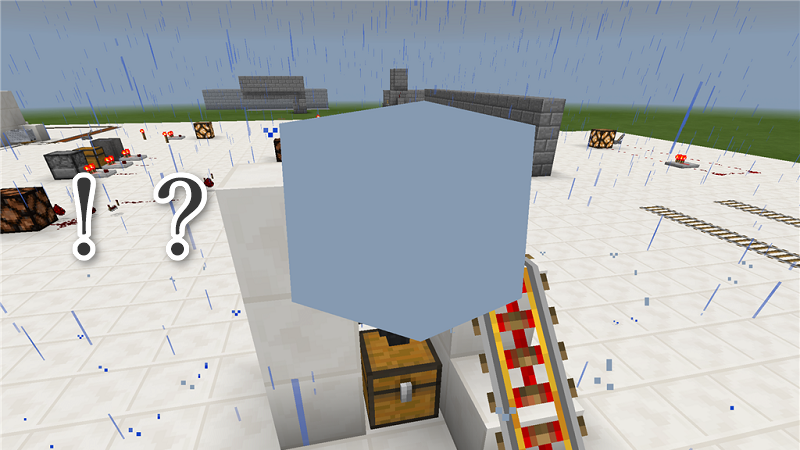
「?」は、これからどんな回路を作るべきなのかを真理値表を作って考えるところです。ちなみに、なぜ出力が「C」と「S」という名前なのかと言うと、「C」がCarry out(繰り上がり)、「S」がSum(合計)という英単語に由来するためです。
真理値表を書く
入力と出力の数が決まったので、それぞれの出力に関して真理値表をかいてみます。真理値表によって、どのような回路を作ればいいのかが分かることに注目してください。
出力Cについての真理値表
まずは、出力C(繰り上がり)について考えます。4つの計算、
- 0+0=0
- 0+1=1
- 1+0=1
- 1+1=10
のうち、繰り上がりがあるのは「1+1=10」だけですね。つまり、入力Aと入力Bが両方とも1のときだけ、出力Cは1になります。つまり、A,B,Cの真理値表は次のようになります。
| 入力A | 入力B | 出力C |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
実はこの真理値表と同じ形のものがこの記事に1回出てきたのですが、お分かりでしょうか?
| 入力A | 入力B | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
AND回路の真理値表と同じ形ですね。つまり、入力Aと入力B、出力Cの間には、AND回路を作ればいいのだと分かります!
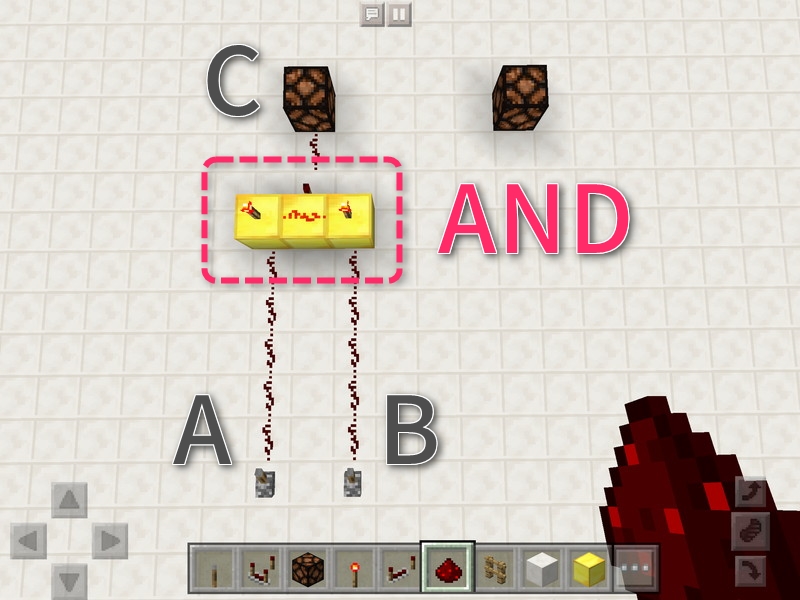
つまり、こうすればよいのです。「?」の一部が埋まりました。
出力Sについての真理値表
次に、出力S(1の位)について考えます。4つの計算、
- 0+0=0
- 0+1=1
- 1+0=1
- 1+1=10
の中で、1の位が1となるのは「0+1=1」、「1+0=1」の2つですね。これを真理値表で表すと、
| 入力A | 入力B | 出力S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
このようになります。これはこのページには出てきていませんが、XOR回路(2つの入力が異なるときONを出力する回路)の真理値表と同じですね。XOR回路について、詳しくは以下をご覧ください。
つまり、入力Aと入力B、出力Sの間には、XOR回路を作ればいいということが分かります。

先ほどすでに作った回路をまたぐ必要があるので、気をつけてください。
なお、XOR回路はコンパクト化のため、コンパレーターを2個使用するタイプにしてあります。詳しく知りたい方はこちら。
完成!
全ての入力と出力をつないだので、これで単純な計算機は完成になります。
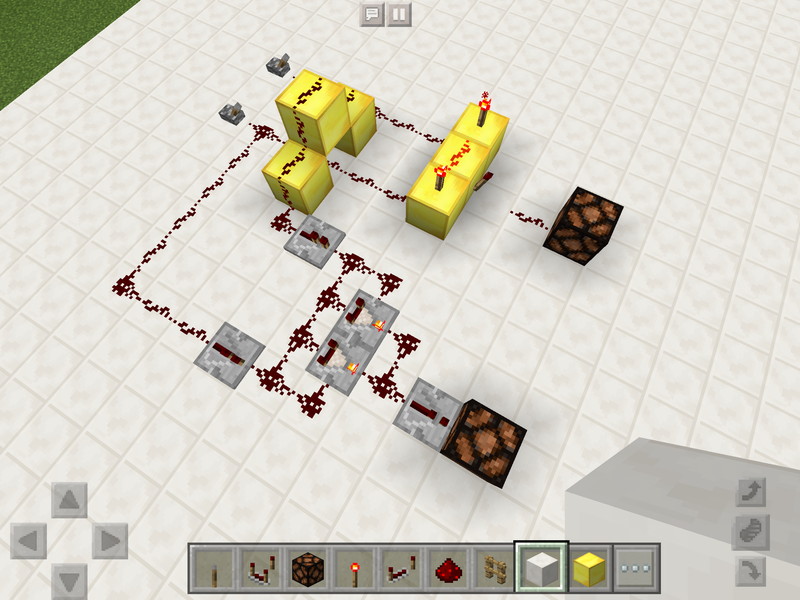
それでは、レバーを動かして動作を確かめてみましょう。
0+0=0
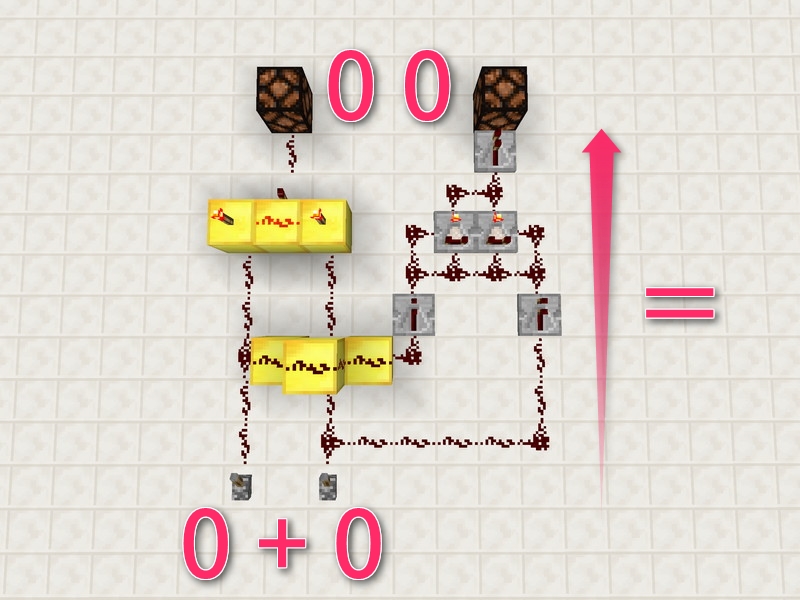
0+1=1
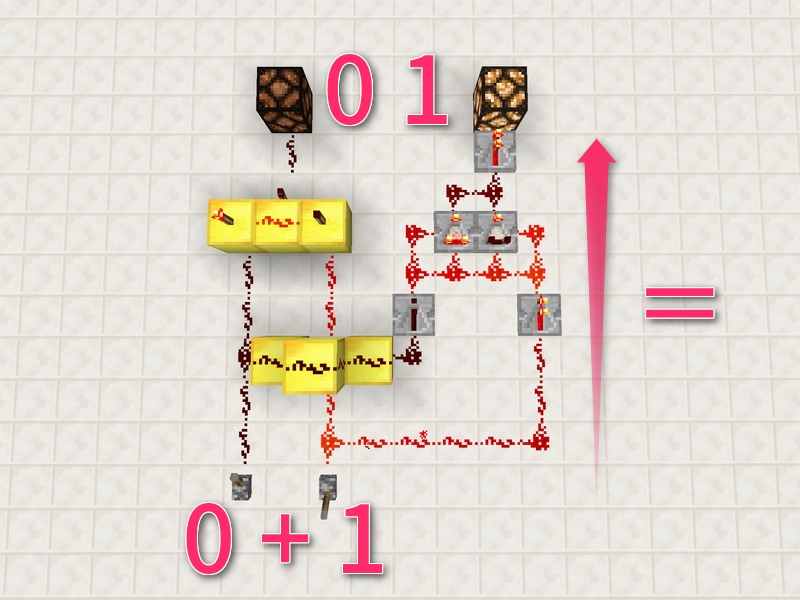
1+0=1
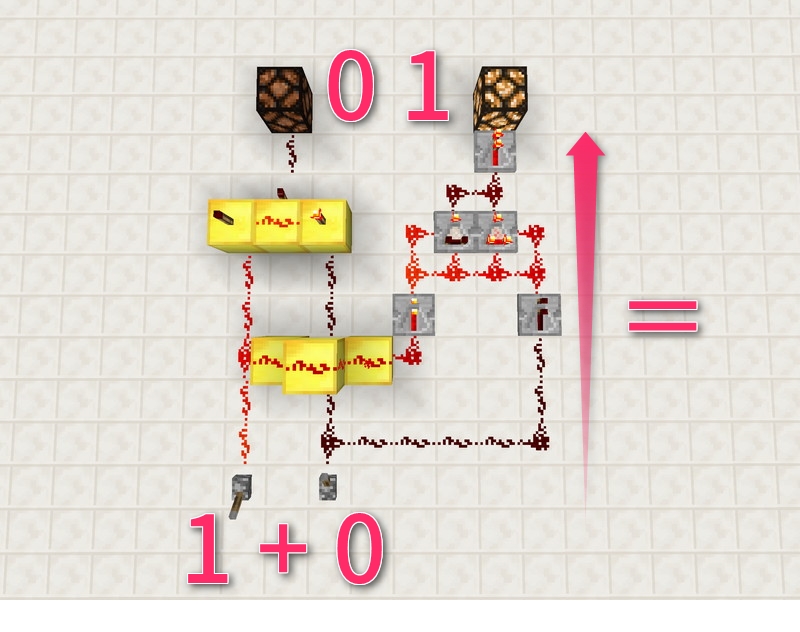
1+1=10
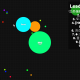
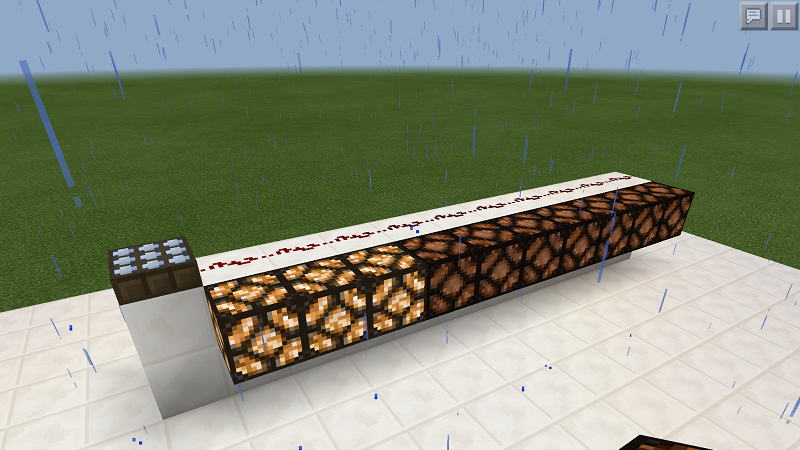
このように、4つ全ての計算を正しくできることが分かりました。これだけではたった4つの計算しかできませんが、この回路は全ての計算機の基本となるもので、ものすごく重要です。半加算器という名前がありますよ。
改善するべき点
半加算器がいくら重要であっても、まだまだ計算機としては性能が低いですよね。例えば、
- 計算できる桁数が少なすぎる
- 2進数での計算しかできない
これらの問題点を解決すると、普段私たちが使っているような計算機が作れますね。これらについても、このブログで解説していく予定ですのでお楽しみに!
ちなみに
半加算器に関する2つの真理値表をまとめると、このようになります。
| 入力A | 入力B | 出力C | 出力S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
これ、実は4つの計算式と形が全く同じです(わかりやすくするため、上のケタの0も書き加えました)。
- 0+0=00
- 0+1=01
- 1+0=01
- 1+1=10
実は必要な計算の式を全部書き出すという行為が、すでに真理値表を作るということと同じことだったんですね。
これを使えば、3つの数を足す計算機というのも作れそうな気がしてきませんか……?これは特にお教えしませんが、興味があればぜひチャレンジしてみてください。
質問をどうぞ
最初にお伝えした通り、この記事の内容に関して何か分からないことがあれば、下のコメント欄にご質問をどうぞ。できる限り分かりやすくなるように書いたのですが、なかなか最初は複雑に思える分野ですので……。
後で見る方々の助けにもなるかもしれないので、ご遠慮なくどうぞ。

























半加算機の説明をありがとうございます。
論理回路利用の発展型を垣間見た気がいたします。
このページの記述について確認したいのですが、
“そして、出力も2つ必要になります”のところで使用している画像では、”10”に対応するレッドストーンランプの表現が、二つとも点灯になっております。
こちらは、左側点灯・右側点灯の誤記ではないでしょうか?
すべて読み進める前だったので、2個点灯の表現は、
計算結果をランプのオンオフを二進数に見立てて表現するのではなく、
点灯の個数=2(10進数)というように、数式の答えを点灯の個数にて表現するのかと勘違いし、
結論まで読み進めるまで首をひねっておりました。
論理式の解説はとてもわかりやすく、
是非ともほかのページも参考にさせていただきます。
全然違う話するけど、「ナギサクラフト」ってどうなったんでしょう?
“必要な入力と出力の数を考える“で10を出力するとき左右両方のランプが点灯していますが左だけ点灯で右は消灯の間違いではないでしょうか?
AND や XOR 回路で半加算器をつくる原理は書籍で読んで知っていたつもりになっていましたが、実際に Minecraft で作ってみる方が理解力は数倍だということを痛感しました。大人の自由研究にとても良い。
高専に進学した新1年生へ
この記事に書かれている知識は、授業で使うので覚えておいてください。特に真理値表やXECULUSIVE-OR回路なども詳しく扱います。後期中間試験で出ます。
ふ~ん エッチじゃん
???
電卓は作れないなあこれだけじゃ